Question

You have a 2m long wire which you will make into a thin coil with N loops to generate a magnetic field of 3mT when the current in the wire is 1.2A. What is the radius of the coils and how many loops, N, are there

Answer 1

radius of the loop = 7.9 mm

number of turns N ≅ 399 turns

Step-by-step explanation:

length of wire L= 2 m

field strength B = 3 mT = 0.003 T

current I = 12 A

recall that field strength B = μnI

where n is the turn per unit length

vacuum permeability μ =
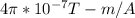`4\pi *10^(-7) T-m/A` = 1.256 x 10^-6 T-m/A

imputing values, we have

0.003 = 1.256 x 10^−6 x n x 12

0.003 = 1.507 x 10^-5 x n

n = 199.07 turns per unit length

for a length of 2 m,

number of loop N = 2 x 199.07 = 398.14 ≅ 399 turns

since there are approximately 399 turns formed by the 2 m length of wire, it means that each loop is formed by 2/399 = 0.005 m of the wire.

this length is also equal to the circumference of each loop

the circumference of each loop =
`2\pi r`

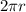
0.005 = 2 x 3.142 x r

r = 0.005/6.284 =
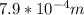`7.9*10^(-4) m` = 0.0079 m = 7.9 mm