The question is incomplete! Complete question along with answer and step by step explanation is provided below.
Question:
How large of a sample of state employees should be taken if we want to estimate with 98% confidence the mean salary to be within $2,000? The population standard deviation is assumed to be $10,500. z-value for 98% confidence level is 2.326.
Answer:
Sample size = n = 150
Explanation:
Recall that the margin of error is given by
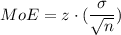
Re-arranging for the sample size (n)
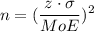
Where z is the value of z-score corresponding to the 98% confidence level.
Since we want mean salary to be within $2,000, therefore, the margin of error is 2,000.
The z-score for a 98% confidence level is 2.326
So the required sample size is
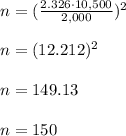
Therefore, we need to take a sample size of at least 150 state employees to estimate with 98% confidence the mean salary to be within $2,000.