Answer:
The probability of getting a sample with 80% satisfied customers or less is 0.0125.
Explanation:
We are given that the results of 1000 simulations, each simulating a sample of 80 customers, assuming there are 90 percent satisfied customers.
Let
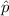 = sample proportion of satisfied customers
= sample proportion of satisfied customers
The z-score probability distribution for the sample proportion is given by;
Z =
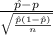 ~ N(0,1)
~ N(0,1)
where, p = population proportion of satisfied customers = 90%
n = sample of customers = 80
Now, the probability of getting a sample with 80% satisfied customers or less is given by = P(
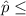 80%)
80%)
P(
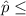 80%) = P(
80%) = P(
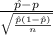

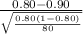 ) = P(Z
) = P(Z
 -2.24) = 1 - P(Z < 2.24)
-2.24) = 1 - P(Z < 2.24)
= 1 - 0.9875 = 0.0125
The above probability is calculated by looking at the value of x = 2.24 in the z table which has an area of 0.9875.