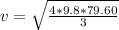Answer:
The center of mass velocity is

Step-by-step explanation:
From the question we are told that
The mass of the cylinder is
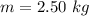
The radius is
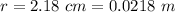
The length is
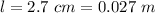
The height of the plane is h = 79.60 m
and the distance covered is
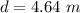
The center of mass velocity o the cylinder when it reaches the bottom is mathematically represented as
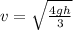
substituting values