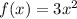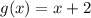Answer:
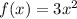
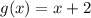
Explanation:
Given
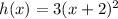
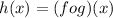
Required
Find f(x) and g(x)
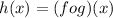
Rewrite h(x)
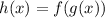
If
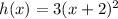
then
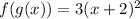
This implies that; the expression in the brackets are equal;
In other words; function g(x) on the left hand side is equal to expression x + 2 on the right hand side
So;
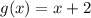
To find f(x), substitute g(x) with x
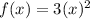
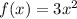
Final solutions are