Question

Simplify 2(a-3)/(a-4)(a-5)+(a-1)/(3-a)(a-4)+(a-2)/(5-a)(a-3)​

Answer 1

`(5)/(x^3-12x^2+47x-60)`

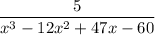
Explanation:

Though it is not what you have written, we think you want to simplify ...

`(2(a-3))/((a-4)(a-5))+((a-1))/((3-a)(a-4))+((a-2))/((5-a)(a-3))\\\\=(2(a-3)^2)/((a-3)(a-4)(a-5))+(-(a-1)(a-5))/((a-3)(a-4)(a-5))+(-(a-2)(a-4))/((a-3)(a-4)(a-5))\\\\=(2(a^2-6a+9)-(a^2-6a+5)-(a^2-6a+8))/(x^3-12x^2+47x-60)\\\\=\boxed{(5)/(x^3-12x^2+47x-60)}`

_____

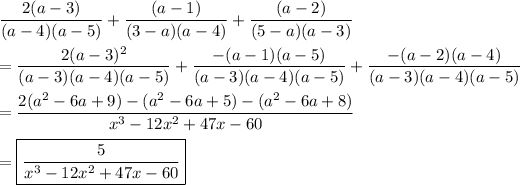
When writing a fraction in plain text, parentheses are needed around the entire denominator. The order of operations tells you that a/bc = (a/b)c, not a/(bc).