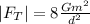Question

The figure shows a system of five objects. Determine the magnitude of the gravitational force acting on the

object placed in the middle of the square.

Select one:
O a. 4Gm2/d2
O b. Gm2/d2
O c. 8Gm2/d2

Answer 1

c.
`|F_T|=8(Gm^2)/(d^2)`

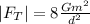
Step-by-step explanation:

In order to calculate the gravitational force on the mass of the center, you take into account the following formula:

`F=G(m_1m_2)/(r)` (1)

Furthermore, you take into account the components of the resultant vector.

By the illustration, you have that the force is given by:

`F_T=F_1+F_2+F_3+F_4\\\\F_1=(Gm_1m)/(r^2)[-cos45\°\hat{i}+sin45\°\hat{j}]\\\\F_2=(Gm_2m)/(r^2)[cos45\°\hat{i}+sin45\°\hat{j}]\\\\F_3=(Gm_3m)/(r^2)[cos45\°\hat{i}-sin45\°\hat{j}]\\\\F_4=(Gm_4m)/(r^2)[-cos45\°\hat{i}-sin45\°\hat{j}]`

where:

m1 = m

m2 = 2m

m3 = m

m4 = 4m

m: mass at the center of the system

The distance r is:

`r=\sqrt{((d)/(2))^2+((d)/(2))^2}=(d)/(√(2))`

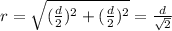
You replace the values for all masses and sum the contributions of all forces:

`F_1=(√(2))/(2)(Gm^2)/(((d^2)/(2)))[-\hat{i}+\hat{j}]=√(2)(Gm^2)/(d^2)[-\hat{i}+\hat{j}]\\\\F_2=(√(2))/(2)(2Gm^2)/(((d^2)/(2)))[\hat{i}+\hat{j}]=2√(2)(Gm^2)/(d^2)[\hat{i}+\hat{j}]\\\\F_3=(√(2))/(2)(Gm^2)/(((d^2)/(2)))[\hat{i}-\hat{j}]=√(2)(Gm^2)/(s^2)[\hat{i}-\hat{j}]\\\\F_4=(√(2))/(2)(4Gm^2)/(((d^2)/(2)))[-\hat{i}-\hat{j}]=4√(2)(Gm^2)/(d^2)[-\hat{i}-\hat{j}]\\\\F_T=-2√(2)(Gm^2)/(d^2)}[\hat{i}+\hat{j}]`

and the magnitude is:

c.
`|F_T|=8(Gm^2)/(d^2)`