Question

. Jayvon bakes two small circular cakes that are 8 inches across their widest point and 3 inches high. He removes the cake from the pans to frost them. Jayvon would like a consistent quarter-inch deep layer of frosting. How many cubic inches of frosting does he need for the cakes if he wants to frost only the top and sides of each cake

Answer 1

20π in³ or 62.832 in³

Explanation:

The surface area for each cake is given by:

`S=\pi r^2+2\pi rh`

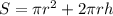
Where 'r' is the radius of each cake (4 inches), and 'h' is the height of each cake (3 inches). Since there are two cakes, the total surface area is:

`A=2*(\pi r^2+2\pi rh)\\A=2*(\pi 4^2+2\pi*4*3)\\A=80\pi\ in^2`

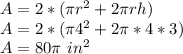
If Jayvon wants a consistent quarter-inch deep layer of frosting covering the surface of the cakes, the volume of frosting required is:

`V=80\pi *0.25\\V=20\pi\ in^3 = 62.832\ in^3`

He needs 20π in³ or 62.832 in³ of frosting.