Question

It is found that, when a dilute gas expands quasistatically from 0.40 to 3.5 L, it does 340 J of work. Assuming that the gas temperature remains constant at 300 K, how many moles of gas are present?

Answer 1

The number of moles of gas present is 0.0629 mol.

Step-by-step explanation:

Given;

initial volume of the gas,
`v_i` = 0.4 L = 0.4 x 10

final volume of the gas,
`v_f` = 3.5 L

work done by the gas, W = 340 J

constant temperature, T = 300 K

gas constant, R = 8.31 J/mol.K

work done by gas at constant temperature is given as;

`W = \int\limits^(v_f)_(v_i) {Pdv} \\\\W = nRT*ln((v_f)/(v_i) )\\\\n = (W)/(RT*ln((v_f)/(v_i) )) \\\\n = (340)/(8.31*300*ln((3.5 )/(0.4) ))\\\\n = 0.0629 \ mol`

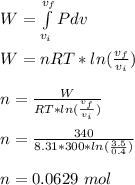
Therefore, the number of moles of gas present is 0.0629 mol.