The picture isn't quite clear, so i have include a clearer one in the attachment below.
We need to determine the altitude of segment BD. From taking a look at the picture I can conclude that these triangle( s ) formed through the camera's positioning are proportional to one another, but here is the evidence -
( By Vertical Angle's Theorem,
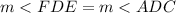
( By Alternate Interior Angle's Theorem,
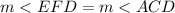
( Respectively by Alternate Interior Angle's Theorem,
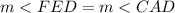
Therefore we can conclude that these triangle are similar to one another, and hence we can create a proportionality as such ( with the lengths ) -
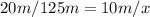
And this " x " is the length of segment BD, which we want to determine -

The altitude with which the camera should be flown is 62.5 meters.
Hope that helps!