Question

The sugar content of the syrup in canned peaches is normally distributed. A random sample of n=25 cans yields a sample standard deviation of s=6.9 milligrams. Construct a 99% one-sided lower confidence bound for the population variance.

Answer 1

99% one-sided lower confidence bound = 26.77

Explanation:

We have to calculate a 99% one-sided lower confidence bound for the population variance.

The sample size is n=25.

The degrees of freedom are then:

`df=n-1=25-1=24`

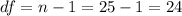
The critical value of the chi-square for this confidence bound is:

`\chi^2_(0.01, \,24)=42.98`

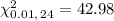
Then, the lower confidence bound can be calculated as:

`LB=((n-1)s^2)/(\chi^2_(0.01,24))=(24\cdot(6.9)^2)/(42.98)=(1,142.64)/(42.68)=26.77`