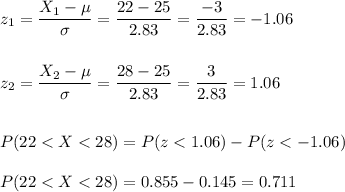Question

The weight of apples is normally distributed. Large apples have a mean of 15 oz and medium apples have a mean of 10 oz. The standard deviation of the weight of both large and medium apples is 2 oz. You select a large apple and a medium apple at random. Let L be the weight of the large apple and M be the weight of a medium apple.

Let X be the total weight of the two apples (X = L + M). The distribution of X is also normal.


Required:
a. Use the rules for means and variances to find the mean and standard deviation of X.
b. What is the probability that the total weight X is between 22 and 28 oz?

Answer 1

a) X has a mean of 25 and a variance of 8.

b) The probability that the total weight X is between 22 and 28 oz is 0.711.

Explanation:

We have to calculate the mean and variance of a sum of random normal variables.

We can apply the rule for mean and variance for sum of independent variables:

`X=L+M\\\\E(X)=E(L+M)=E(L)+E(M)\\\\V(X)=V(L+M)=V(L)+V(M)-2CoV(L,M)=V(L)+V(M)`

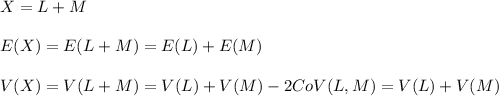
Then, the mean and variance of X is:

`E(X)=E(L)+E(M)=15+10=25\\\\\\V(X)=V(L)+V(M)=2^2+2^2=4+4=8\\\\\sigma_x=√(V(X))=√(8)\approx2.83`

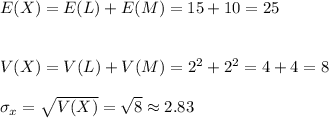
We can calculate the probability that X is between 22 and 28 as:

`z_1=(X_1-\mu)/(\sigma)=(22-25)/(2.83)=(-3)/(2.83)=-1.06\\\\\\z_2=(X_2-\mu)/(\sigma)=(28-25)/(2.83)=(3)/(2.83)=1.06\\\\\\P(22<X<28)=P(z<1.06)-P(z<-1.06)\\\\P(22<X<28)=0.855-0.145=0.711`