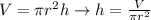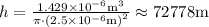Question

We would like to make a golden standard kilogram in the shape of circular cylinder. The density of gold is 19.32 g/cm3. a) Find the volume of the kilogram standard of gold in cubic meter. b) In order to minimize the effect of surface contamination, the height of this golden standard kilogram is equal to its diameter. Find the height of this golden standard kilogram in mm.

Answer 1

Step-by-step explanation:

a) Using the provided information about the density of gold, the sample size, thickness, and the following equations and comersion factors, find the area of the gold leaf:

`V=l \cdot w \cdot h=A \cdot h\\m=\rho \cdot V`

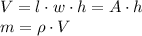
Gold
`_(\rho)=19.32 \mathrm{g} / \mathrm{cm}^(3)`

`1 \mu=10^(-6) \mathrm{m}`

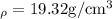
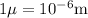
First, find the volume of the sample and then find the area of the sample.

`V=(m)/(\rho)=\frac{27.6 \mathrm{g}}{19.32 \mathrm{g} / \mathrm{cm}^(3)} \cdot\left(\frac{0.01 \mathrm{m}}{1 \mathrm{cm}}\right)^(3)`
`=\frac{1.429 * 10^(-6) \mathrm{m}^(3)}`

`V=A \cdot h \rightarrow A=(V)/(h)=\frac{1.429 * 10^(-6) \mathrm{m}^(3)}{10^(-6) \mathrm{m}} \approx 1.429 \mathrm{m}^(2)`

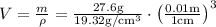
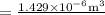
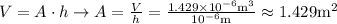
b. Using the provided information from part
`a` ), the radius of the cylinder, and the following equation for the volume of a cylinder, find the length of the fiber :

`V=\pi r^(2) h \rightarrow h=(V)/(\pi r^(2))`

`h=\frac{1.429 * 10^(-6) \mathrm{m}^(3)}{\pi \cdot\left(2.5 * 10^(-6) \mathrm{m}\right)^(2)} \approx 72778 \mathrm{m}`