Question

Let f be defined as shown. Which statement is

true?
Answers
The inverse of f exists
The inverse of f does not exists

Answer 1

`\boxed{\sf \ \ \ the \ inverse \ of \ f \ does \ not\ exist \ \ \ }`

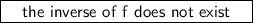
Explanation:

hello,

for one x you cannot get several values of f(x), otherwise this is not a function

as 6 and 7 gives 0 it means that

f(6)=f(7)=0 which is fine for f

but then for
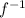`f^(-1)` it would mean that 0 has two different images

and this is not possible

so the inverse of f does not exist

hope this helps