Answer:
The average speed on this trip was 46.15 mph. The correct option is A.
Explanation:
In order to calculate the average speed, we need to apply the following formula:
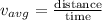
We were given the distance between the two cities in miles, therefore we can directly apply it to the expression. Although the time was given in the hh:mm 12 h format and we need a diference in hours, so we will convert that as shown below:
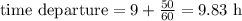
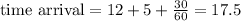
The elapsed time of the trip is the difference between these:
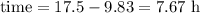
We can now apply it to the formula:

The average speed on this trip was 46.15 mph. The correct option is A.