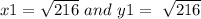Answer:
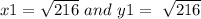
Explanation:
Let the first number is x1 and other number is y1 then
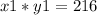
Therefore
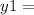
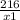
also there sum is
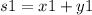 ....Eq(1)
....Eq(1)
Putting the value of y1 in the previous equation
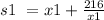 ........Eq(2)
........Eq(2)
Differentiate the the Eq(2) with respect to x1 we get
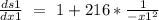
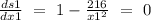
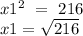
Putting the value of X1 in Eq(1) we get
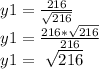
So