Question

The polygon below represents a regular octagon.

Calculate the following angles. You must show your working.

Answer 1

a). x = 135°

b). y = 45°

c). z = 67.5°

Explanation:

Since sum of interior angles of a regular polygon is represented by,

Sum of interior angles = (n - 2) × 180°

Here n = number of sides

For a regular octagon, n = 8

Sum of interior angles = (8 - 2) × 180° = 1080°

And measure of one interior angles =
`\frac{\text{Sum of interior angles}}{n}`

x =
`(1080)/(8)`

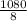
x = 135°

From the figure attached,

Angle C has been divided in 6 equal parts,

Therefor, m∠ECD =
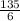`(135)/(6)` = 22.5°

Since ∠ECD ≅ ∠CED,

m∠CED = 22.5°

Since m∠E = 135°

m∠FEC = 135 - 22.5 = 112.5°

In ΔFEC,

m∠FEC + m∠ECF + m∠CFE = 180°

112.5 + 22.5 + z = 180

z = 180 - 135

z = 45°

Similarly, in ΔCGF,

m∠CGF + m∠CFG + m∠GCF = 180°

(135 - y)° + (135 - z)° + 22.5° = 180°

270 - (y + z) + 22.5 = 180

292.5 - (y + 45) = 180

247.5 - y = 180

y = 247.5 - 180

y = 67.5°