Answer:
The amount in the account at the end of three years will be $59,861.
Explanation:
The formula to compute the amount at the end of t years, compounded continuously is:
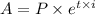
Here,
A = Amount at the end
P = Principal amount
i = interest rate
t = number of years.
It is provided that:
P = $50,000
i = 6%
t = 3 years
Compute the amount in the account at the end of three years as follows:
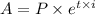
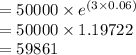
Thus, the amount in the account at the end of three years will be $59,861.