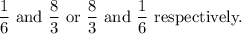Answer:
Explanation:
The numbers x,
 and y are the first three terms of an arithmetic progression.
and y are the first three terms of an arithmetic progression.
For three consecutive terms, a, b and c of an arithmetic sequence:
The arithmetic mean,
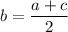
Therefore:

The numbers x,
 and y are three consecutive terms of a geometric progression.
and y are three consecutive terms of a geometric progression.
For three consecutive terms, a, b and c of a geometric sequence:
The geometric mean,

Therefore:

Substituting
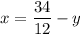 derived above, we have:
derived above, we have:
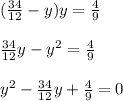
This is a quadratic equation which we can then solve for y.
Using a calculator, we obtain:


Therefore, the values of x and y are: