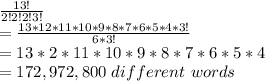Question

How many different "words" can be made from the given word by re-arranging the letters? 1. KINDNESS 2. MATHEMATICIAN

Answer 1

Explanation:

Permutation has to do with arrangement.

To form different word by rearranging the word KINDNESS, this can be done in the following way;

The total letters present in kindness = 8 letters

Repeated letters are 2N's and 2S's

The arrangement is done in
`(8!)/(2!2!)` ways

`= (8!)/(2!2!) \\= (8*7*6*5*4*3*2!)/(2!*2)\\ = 8*7*3*5*4*3\\= 10,080 \ different\ words`

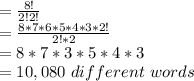
For MATHEMATICIAN;

The total letters present in kindness = 13 letters

Repeated letters are 2M's, 2T'S 2I'sand 3A's

The number of words formed =

`(13!)/(2!2!2!3!) \\= (13*12*11*10*9*8*7*6*5*4*3!)/(6*3!)\\= 13*2*11*10*9*8*7*6*5*4\\= 172,972,800\ different\ words`