Question

A geometric sequence has an initial value of 3 and a common ratio of 2. Which function(s) or formula(s) could represent this situation? Select all that apply.

Answer 1

The functions that represent this situation are A.
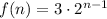`f(n)=3\cdot 2^(n-1)` and C.
`a(n)=a(n-1)\cdot 2; a(1)=3`.

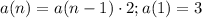Explanation:

A geometric sequence goes from one term to the next by always multiplying or dividing by the same value.

In geometric sequences, the ratio between consecutive terms is always the same. We call that ratio the common ratio.

This is the explicit formula for the geometric sequence whose first term is k and common ratio is r:

`a(n)=k\cdot r^(n-1)`

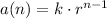
This is the recursive formula of that sequence:

`a(1)=k\\\\a(n)=a(n-1)\cdot r`

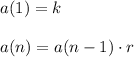
We know that the first term is k = 3 and the common ratio is r = 2. Therefore,

The explicit formula is
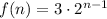`f(n)=3\cdot 2^(n-1)` and the recursive formula is
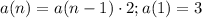`a(n)=a(n-1)\cdot 2; a(1)=3`.