Question

g The radius of a spherical ball increases at a rate of 3 m/s. At what rate is the volume changing when the radius is equal to 2 meters

Answer 1

dV/dt = 150.79 m^3/s

Step-by-step explanation:

In order to calculate the rate of change of the volume, you calculate the derivative, respect to the radius of the sphere, of the volume of the sphere, as follow:

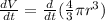`(dV)/(dt)=(d)/(dt)((4)/(3)\pi r^3)` (1)

r: radius of the sphere

You calculate the derivative of the equation (1):

`(dV)/(dt)=(d)/(dt)((4)/(3)\pi r^3)=3(4)/(3)\pi r^2(dr)/(dt)=4\pi r^2(dr)/(dt)\\\\(dV)/(dt)=4\pi r^2(dr)/(dt)`(2)

where dr/dt = 3m/s

You replace the values of dr/dt and r=2m in the equation (2):

`(dV)/(dt)=4\pi (2m)^2(3(m)/(s))=150.79(m^3)/(s)`

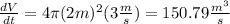
The rate of change of the sphere, when it has a radius of 2m, is 150.79m^3/s