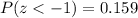Question

The mean amount spent by a family of four on food is $500 per month with a standard deviation of $75. Assuming that the food costs are normally distributed, what is the probability that a family spends less than $425 per month?​

Answer 1

`z=(x- \mu)/(\sigma)`

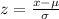
And replacing we got:

`z=(425-500)/(75)= -1`

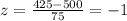
And we can calculate this probabilit using the normal standard distribution or excel and we got:

`P(z<-1)= 0.159`

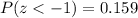
Explanation:

If we define the random variable of interest "the amount spent by a family of four of food per month" and we know the following parameter:

`\mu = 500, \sigma = 75`

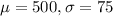
And we want to find the following probability:

`P(X<425)`

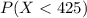
And we can use the z score formula given by:

`z=(x- \mu)/(\sigma)`

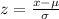
And replacing we got:

`z=(425-500)/(75)= -1`

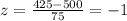
And we can calculate this probabilit using the normal standard distribution or excel and we got:

`P(z<-1)= 0.159`