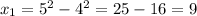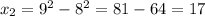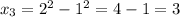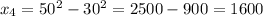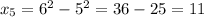Question

Please its very urgent :( Name five whole numbers that can be expressed as the difference of two perfect squares. Show the math!

Answer 1

9, 17, 3, 1600, 11

Explanation:

Difference of two perfect squares:

`a^2-b^2=(a-b)(a+b)`

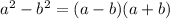
It seems that you want some

`x=a^2-b^2, x \in \mathbb{Z}_(\ge 0)`

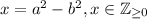
Note: there's no official symbol for the set of whole numbers, I've already seem
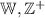`\mathbb{W}, \mathbb{Z}^+`, as well.

`5^2-4^2=25-16=9`

There are infinitely many numbers that can satisfy the condition given.

The only condition is that
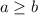`a\geq b`, once we are considering whole numbers and not integers.

`x_(1)=5^2-4^2=25-16=9`

`x_(2)=9^2-8^2=81-64=17`

`x_(3)=2^2-1^2=4-1=3`

`x_(4)=50^2-30^2=2500-900=1600`

`x_(5)=6^2-5^2=36-25=11`