Answer:
The two factors of the first number are -4 and 9.
Explanation:
We're given:
- Two numbers have a product of -36
- The same two numbers have a sum of 5
Let the two numbers be a and b:
Solving for b
Isolate a in the second equation and solve for b:
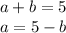
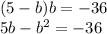
Arrange in
 format:
format:
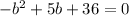
Divide both sides by -1:
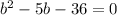
Factor:
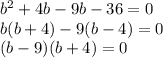
Solve for b using the zero product property:
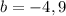
Solve for a
Substitute b back into the second equation to solve for a:
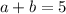
First, let b = -4:
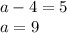
Let b = 9:
