Question

A student sits on a rotating stool holding two 1 kg objects. When his arms are extended horizontally, the objects are 0.9 m from the axis of rotation, and he rotates with angular speed of 0.61 rad/sec. The moment of inertia of the student plus the stool is 6 kg m^2 and is assumed to be constant. The student then pulls the objects horizontally to a radius 0.39 m from the rotation axis.

Required:
a. Calculate the final angular speed of the student. Answer in units of rad/s.
b. Calculate the change in kinetic energy of the system. Answer in units of J.

Answer 1

a) the final angular speed is 0.738 rad/s

b) the change in kinetic energy = 0.3 J

Step-by-step explanation:

the two 1 kg objects have a total mass of 2 x 1 = 2 kg

radius of rotation of the objects = 0.9 m

moment of inertial of the student and the chair = 6 kg-m^2

initial angular speed of rotation of the sitting student and object system ω1 = 0.61 rad/s

final angular speed of rotation of the sitting student and object system ω2 = ?

moment of inertia of the rotating object is

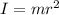`I = mr^(2)` = 2 x
`0.9^(2)` = 1.62 kg-m^2

total moment of inertia of sitting student and object system will be

==> 6 + 1.62 = 7.62 kg-m^2

The initial angular momentum of the sitting student and object system will be calculated from

==> Iω1 = 7.62 x 0.61 = 4.65 kg-rad/s-m^2

if the radius of rotation of the object is reduced to 0.39 m,

new moment of inertia of the rotating object will be

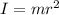`I = mr^(2)` = 2 x
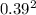`0.39^(2)` = 0.304 kg-m^2

new total moment of inertia of the sitting student and object system will be

==> 6 + 0.304 = 6.304 kg-m^2

The final momentum of the sitting student and object system will be calculated from

==> Iω2 = 6.304 x ω2 = 6.304ω2

According to conservation of angular momentum, initial momentum of the system must be equal to the final momentum of the system. Therefore,

4.65 = 6.304ω2

ω2 = 4.65/6.30 = 0.738 rad/s

b) Rotational kinetic energy of the system =
`(1)/(2) Iw^(2)`

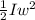
for the initial conditions, kinetic energy is

==>
`(1)/(2) Iw1^(2)` =
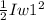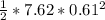`(1)/(2)* 7.62*0.61^(2)` = 1.417 J

for the final conditions, kinetic energy is

==>
`(1)/(2) Iw1^(2)` =
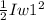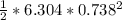`(1)/(2)*6.304*0.738^(2)` = 1.717 J

change in kinetic energy = final KE - initial KE

==> 1.717 - 1.417 = 0.3 J