Question

Find the indicated limit, if it exists. (1 point) limit of f of x as x approaches 9 where f of x equals x plus 9 when x is less than 9 and f of x equals 9 minus x when x is greater than or equal to 9

Answer 1

Explanation:

For the limit of a function to exist, then the right hand limit of the function must be equal to its left hand limit as shown;

If the function is f(x), for f(x) to exist then;

`\lim_(n \to a^(+) ) f(x) = \lim_(n \to a^(-) ) f(x) = \lim_(n \to a ) f(x)`

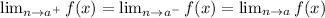
Given the function;

`f(x) = \left \{ {{x+9\ x<9} \atop {9-x \ x \geq 9}} \right\\`

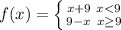
Lets check if the above statement is true.

The right hand limit of the function occurs at x> 9

f(x) = 9-x

`\lim_(x \to 9+) (9-x)\\= 9-9\\= 0`

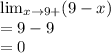
The left hand limit occurs at x<9

f(x) = x+9

`\lim_(x \to 9^(-) ) (x+9)\\= 9+9\\= 18`

From the above calculation, it can be seen that
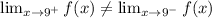`\lim_(x \to 9^(+) ) f(x) \\eq \lim_(x \to 9^(-) ) f(x)`, this shows that the function given does not exist at the given point.