Question

Can someone help me please

Answer 1

`a_(n) = 12 -3(n-1)`

Explanation:

`a_(1) = 12\\a_(n) = a_(n-1) - 3`

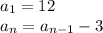
we have to find formula for nth term of series for this problem

`a_(1) = 12\\a_(2) = a_(2-1) - 3 = a_(1) -3 = 12 -3 = 9\\a_(3) = a_(3-1) - 3 = a_(2) -3 = 9 -3 = 6`

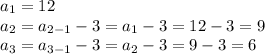
Thus, we see series is 12, 9 ,6

Thus, we can see that series is decreasing by unit of 3.

and we know that when there is in increase or decrease in series by a a constant number then series is arithmetic progression series.

Hence, this is a decreasing AP series

In AP

nth term is given

nth term = a+(n-1)d

where a is the first term

d is the common difference

common difference is given by = nth term - (n-)th term

lets take 2nd and 1st term to get common difference.

d = 9-12 = -3

(note: this was obvious by looking at series itself that d is -3 as series was decreasing by 3 unit)

a = 12

thus, nth term = a +(n-1)d

nth term = 12 +(n-1)(-3)

nth term = 12 -3(n-1)

writing this in form of
`a_(n)`

`a_(n) = 12 -3(n-1)` Answer