Question

What are the solutions to the following system of equations? y = x2 + 12x + 30 8x − y = 10 (2 points) (−4, −2) and (2, 5) (−2, −4) and (2, 5) (−2, −4) and (5, 2) No real solutions

Answer 1

No real solution

Explanation:

Given

`y = x^2 + 12x + 30`

`8x - y = 10`

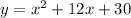
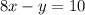
Required

Find x and y

Make y the subject of formula in
`8x - y = 10`

`8x - y + y = 10 + y`

`8x = 10 + y`

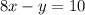
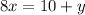
Subtract 10 from both sides

`8x - 10 = 10 - 10 + y`

`8x - 10 = y`

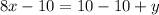
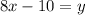
Substitute 8x - 10 for y in
`y = x^2 + 12x + 30`

`8x - 10 = x^2 + 12x + 30`

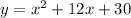
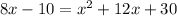
Subtract (8x - 10) from both sides

`8x - 10 - (8x - 10) = x^2 + 12x + 30 - (8x - 10)`

`0 = x^2 + 12x + 30 - (8x - 10)`

`0 = x^2 + 12x + 30 - 8x + 10`

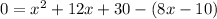
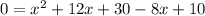
Collect like terms

`0 = x^2 + 12x -8x + 30+ 10`

`0 = x^2 + 4x + 40`

`x^2 + 4x + 40 = 0`

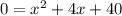
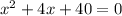
At this point, we have a quadratic equation;

First, we'll check if the quadratic equation has real solution using:

`d = b^2 - 4ac`

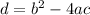
Where a = 1; b = 4 and c= 40

`d = 4^2 - 4 * 1 * 40`

`d = 16 - 160`

`d = -144`

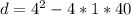
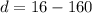
Because the value of d is negative, then we can conclude that the solution has no real solution