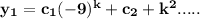Answer:
The answer to this question can be defined as follows:
Explanation:
The given equation is:

put,
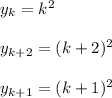
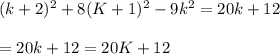
hence y_k=k^2 is its solution.
Now,

the symbol form is:
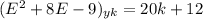

The general solution is:
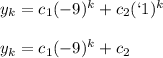
The complete solution is:

The answer is option b:
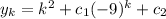
After solve the complete solution is: