Question

Of 41 bank customers depositing a check, 22 received some cash back. Construct a 90 percent confidence interval for the proportion of all depositors who ask for cash back. (Round your answers to 4 decimal places.)

Answer 1

CI: {0.4085; 0.6647}

Explanation:

The confidence interval for a proportion (p) is given by:

`p \pm z*\sqrt{((1-p)*p)/(n) }`

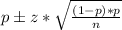
Where n is the sample size, and z is the z-score for the desired confidence interval. The score for a 90% confidence interval is 1.645. The proportion of depositors who ask for cash back is:

`p=(22)/(41)=0.536585`

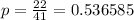
Thus the confidence interval is:

`0.536585 \pm 1.645*\sqrt{((1-0.536585)*0.536585)/(41)}\\0.536585 \pm 0.128109\\L=0.4085\\U=0.6647`

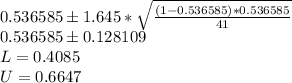
The confidence interval for the proportion of all depositors who ask for cash back is CI: {0.4085; 0.6647}