Answer:
1. The 99% confidence interval is from 941.527 to 958.473
2. The 99% confidence interval is from 933.054 to 966.946
3. The 99% confidence interval is from 916.108 to 983.892
Explanation:
The confidence interval is given by
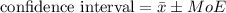
Where
 is the sample mean and Margin of error is given by
is the sample mean and Margin of error is given by
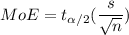
Where n is the sample size,
s is the sample standard deviation,
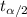 is the t-score corresponding to some confidence level
is the t-score corresponding to some confidence level
The t-score corresponding to 99% confidence level is
Significance level = α = 1 - 0.99 = 0.01/2 = 0.005
Degree of freedom = n - 1 = 13 - 1 = 12
From the t-table at α = 0.005 and DoF = 12
t-score = 3.055
1. 99% Confidence Interval when s = 10
The margin of error is
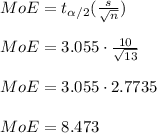
So the required 99% confidence interval is

The 99% confidence interval is from 941.527 to 958.473
2. 99% Confidence Interval when s = 20
The margin of error is
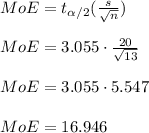
So the required 99% confidence interval is
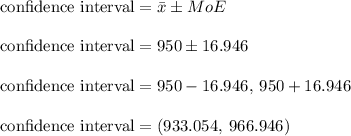
The 99% confidence interval is from 933.054 to 966.946
3. 99% Confidence Interval when s = 40
The margin of error is
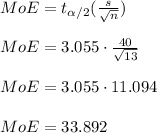
So the required 99% confidence interval is
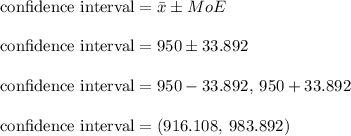
The 99% confidence interval is from 916.108 to 983.892
As the sample standard deviation increases, the range of confidence interval also increases.