Question

Use Lagrange multipliers to find the volume of the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the planex + 9y + 4z = 27.

Answer 1

81/4

Explanation:

From the given information; we are to use Lagrange multipliers to find the volume of the largest rectangular box

The coordinate planes and the vertex given in the plane is x + 9y + 4z = 27.

By applying Lagrange multipliers, we have;

`fx = \lambda gx`

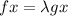
where;

`f: V = xyz`

`g : x + 9y + 4z = 27`

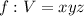
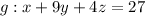
From;
`fx = \lambda gx`

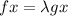
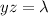`yz = \lambda` --------- equation (1)

From;
`fy = \lambda gy`

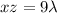`xz = 9 \lambda` --------- equation (2)

From;
`fz = \lambda gz`

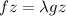
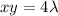`xy = 4 \lambda` --------- equation (3)

Comparing and solving equation (1),(2) and (3);

`\lambda x = 9 \lambda y = 4 \lambda z`

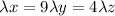
divide through by
`\lambda`

x = 9 y = 4z

3x = 27

x = 27/3

x = 9

From x = 9y

9 = 9 y

y = 9/9

y = 1

From

x = 4z

9 = 4 z

z = 9/4

Thus; the Volume of the largest rectangular box = 9 × 1 × 9/4

= 81/4