Question

The marketing research department of a computer company used a large city to test market the​ firm's new laptop. The department found the relationship between price p​ (dollars per​ unit) and the demand x​ (units per​ week) was given approximately by the following equation.

p= 1275 = 0.17x^2 0 < x < 80

So, weekly revenue can be approximated by the following equation.

R(x)= rp = 1275x- 0.17x^3 0 < x <80

Required:
a. Find the local extrema for the revenue function. What is/are the local maximum/a?
b. On which intervals is the graph of the revenue function concave upward?
c. On which intervals is the graph of the revenue function concave downward?

Answer 1

a. Local maximum = 50 units per week.

b. The graph is never concave upward.

c. (0, 80)

Explanation:

a. The revenue function is:

`R(x) = 1275x-0.17x^3`

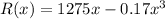
The derivate of the revenue function for which R'(x) = 0 gives us the local extrema:

`R'(x) =0= 1275-0.51x^2\\x=√(2,500)\\x=50`

The second derivate of the revenue function determines if x =50 is local maximum or minimum:

`R''(x) = -1.02x\\R''(50) = -1.02*50=-51\\`

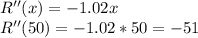
Since the second derivate yields a negative value, x = 50 units per week is a local maximum.

b. Since there are no local minimums in the range of 0 < x < 80, the graph is never concave upward.

c. Since there is only one local maximum in the range of 0 < x < 80, the graph is concave downward from x>0 to x<80 or (0, 80)