Question

A large mixing tank initially contains 1000 gallons of water in which 30 pounds of salt have been dissolved. Another brine solution is pumped into the tank at the rate of 4 gallons per minute, and the resulting mixture is pumped out at the same rate. The concentration of the incoming brine solution is 2 pounds of salt per gallon. If represents the amount of salt in the tank at time t, the correct differential equation for A is:__________.A.) dA/dt = 4 - .08AB.) dA/dt = 8 -.04AC.) dA/dt = 4-.04AD.) dA/dt = 2-.04AE.) dA/dt = 8-.02A

Answer 1

(B)
`(dA)/(dt)=8-0.004A`

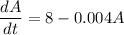
Explanation:

Volume of fluid in the tank =1000 gallons

Initial Amount of Salt in the tank, A(0)= 30 pounds

Incoming brine solution of concentration 2 pounds of salt per gallon is pumped in at a rate of 4 gallons per minute.

Rate In=(concentration of salt in inflow)(input rate of brine)

`=(2(lbs)/(gal))( 4(gal)/(min))=8(lbs)/(min)`

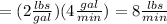
The resulting mixture is pumped out at the same rate, therefore:

Rate Out =(concentration of salt in outflow)(output rate of brine)

`=((A(t))/(1000))( 4(gal)/(min))=(A)/(250)`

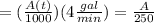
Therefore:

The rate of change of amount of salt in the tank,

`(dA)/(dt)=$Rate In-Rate out\\(dA)/(dt)=8-(A)/(250)\\(dA)/(dt)=8-0.004A`