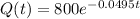Question

Every chemical element goes through natural exponential decay, which means that over time its atoms fall apart. The speed of each element's decay is described by its half-life, which is the amount of time it takes for the number of radioactive atoms of this element to be reduced by half.

The half-life of the isotope beryllium-11 is 14 seconds. A sample of beryllium-11 was first measured to have 800 atoms. After t seconds, there were only 50 atoms of this isotope remaining.

Requried:
Write an equation in terms of t that models the situation.

Answer 1

`Q(t) = 800e^(-0.0495t)`

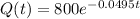
Explanation:

The amount of the isotope after t seconds is given by the following exponential equation:

`Q(t) = Q(0)e^(-rt)`

In which Q(0) is the initial amount and r is the decay rate.

A sample of beryllium-11 was first measured to have 800 atoms.

This means that
`Q(0) = 800`

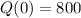
The half-life of the isotope beryllium-11 is 14 seconds.

This means that
`Q(14) = 0.5Q(0)`

We use this to find r.

`Q(t) = Q(0)e^(-rt)`

`0.5Q(0) = Q(0)e^(-14r)`

`e^(-14r) = 0.5`

`\ln{e^(-14r)} = ln(0.5)`

`-14r = ln(0.5)`

`r = -(ln(0.5))/(14)`

`r = 0.0495`

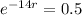
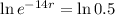
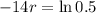
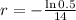
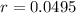
So

`Q(t) = Q(0)e^(-rt)`

`Q(t) = 800e^(-0.0495t)`