Answer:
The velocity imparted to barge 2 just after the car has come to rest on the barge = 0.096 km/h
Step-by-step explanation:
Mass of the two barges,
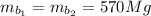 = 570000 kg
= 570000 kg
Mass of the car,
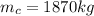
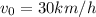
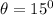
The horizontal component of car velocity:
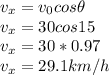
The driver brings his car to rest relative to barge 2 at B:
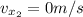
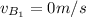
Applying the principle of conservation of momentum:
