Step-by-step explanation:
Formula to calculate the energy stored in a capacitor when it is filled with air is,
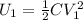 ]
]
Here,
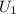 is the energy stored in a capacitor when it is filled with air.
is the energy stored in a capacitor when it is filled with air.
 is the parallel plate capacitor.
is the parallel plate capacitor.
[/tex]V_{\mathrm{i}}[/tex] is the initial potential difference.
Substitute
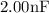 for
for
 and
and
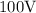 for
for
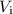 to find the
to find the
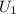
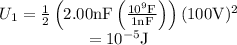 ]
]
Formula to calculate the energy stored in a capacitor when it is filled with dielectric is,