Answer:
1. H0: P1 = P2
2. Ha: P1 ≠ P2
3. pooled proportion p = 0.542
4. P-value = 0.0171
5. The null hypothesis failed to be rejected.
At a signficance level of 0.01, there is not enough evidence to support the claim that there is significant difference between the exercise habits of Science majors and Math majors .
6. The 99% confidence interval for the difference between proportions is (-0.012, 0.335).
Explanation:
We should perform a hypothesis test on the difference of proportions.
As we want to test if there is significant difference, the hypothesis are:
Null hypothesis: there is no significant difference between the proportions (p1-p2 = 0).
Alternative hypothesis: there is significant difference between the proportions (p1-p2 ≠ 0).
The sample 1 (science), of size n1=135 has a proportion of p1=0.607.
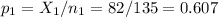
The sample 2 (math), of size n2=92 has a proportion of p2=0.446.
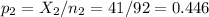
The difference between proportions is (p1-p2)=0.162.
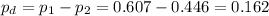
The pooled proportion, needed to calculate the standard error, is:
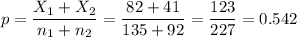
The estimated standard error of the difference between means is computed using the formula:
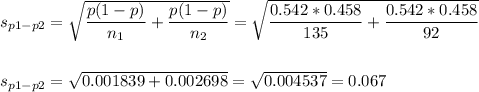
Then, we can calculate the z-statistic as:
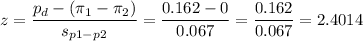
This test is a two-tailed test, so the P-value for this test is calculated as (using a z-table):
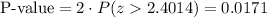
As the P-value (0.0171) is bigger than the significance level (0.01), the effect is not significant.
The null hypothesis failed to be rejected.
At a signficance level of 0.01, there is not enough evidence to support the claim that there is significant difference between the exercise habits of Science majors and Math majors .
We want to calculate the bounds of a 99% confidence interval of the difference between proportions.
For a 99% CI, the critical value for z is z=2.576.
The margin of error is:
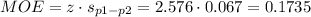
Then, the lower and upper bounds of the confidence interval are:
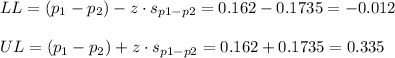
The 99% confidence interval for the difference between proportions is (-0.012, 0.335).