Question

Evaluate the following definite integral.

10
∫ 13y/ y^2-9y-22 .dy
-1

Answer 1

`\displaystyle \int\limits^(10)_(-1) {(13y)/(y^2 - 9y - 22)} \, dy = -9 \ln (12)`

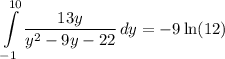
General Formulas and Concepts:

Pre-Calculus

• Partial Fraction Decomposition

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Integration

• Integrals

Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

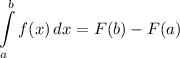
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

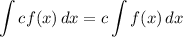
Integration Property [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

U-Substitution

Explanation:

Step 1: Define

Identify

`\displaystyle \int\limits^(10)_(-1) {(13y)/(y^2 - 9y - 22)} \, dy`

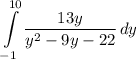
Step 2: Integrate Pt. 1

1. [Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int\limits^(10)_(-1) {(13y)/(y^2 - 9y - 22)} \, dy = 13\int\limits^(10)_(-1) {(y)/(y^2 - 9y - 22)} \, dy`
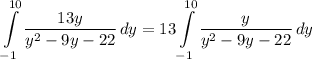
2. [Integrand] Factor:
   `\displaystyle \int\limits^(10)_(-1) {(13y)/(y^2 - 9y - 22)} \, dy = 13\int\limits^(10)_(-1) {(y)/((y - 11)(y + 2))} \, dy`

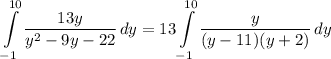
Step 3: integrate Pt. 2

1. [Integrand] Split [Partial Fraction Decomp]:
   `\displaystyle (y)/((y - 11)(y + 2)) = (A)/(y - 11) + (B)/(y + 2)`
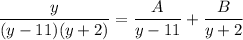
2. [Decomp] Rewrite:
   `\displaystyle y = A(y + 2) + B(y - 11)`
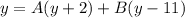
3. [Decomp] Substitute in y = -2:
   `\displaystyle -2 = A(-2 + 2) + B(-2 - 11)`
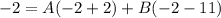
4. Simplify:
   `\displaystyle -2 = -13B`
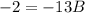
5. Solve:
   `\displaystyle B = (2)/(13)`
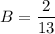
6. [Decomp] Substitute in y = 11:
   `\displaystyle 11 = A(11 + 2) + B(11 - 11)`
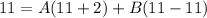
7. Simplify:
   `\displaystyle 11 = 13A`
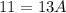
8. Solve:
   `\displaystyle A = (11)/(13)`
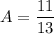
9. [Split Integrand] Substitute in variables:
   `\displaystyle (y)/((y - 11)(y + 2)) = ((11)/(13))/(y - 11) + ((2)/(13))/(y + 2)`

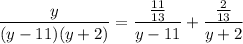
Step 4: Integrate Pt. 3

1. [Integral] Rewrite [Split Integrand]:
   `\displaystyle \int\limits^(10)_(-1) {(13y)/(y^2 - 9y - 22)} \, dy = 13\int\limits^(10)_(-1) {\bigg( ((11)/(13))/(y - 11) + ((2)/(13))/(y + 2) \bigg)} \, dy`
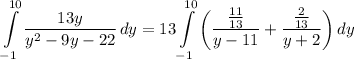
2. [Integral] Rewrite [Integration Property - Addition/Subtraction]:
   `\displaystyle \int\limits^(10)_(-1) {(13y)/(y^2 - 9y - 22)} \, dy = 13 \bigg[ \int\limits^(10)_(-1) {((11)/(13))/(y - 11)} \, dy + \int\limits^(10)_(-1) {((2)/(13))/(y + 2)} \, dy \bigg]`
3. [Integrals] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int\limits^(10)_(-1) {(13y)/(y^2 - 9y - 22)} \, dy = 13 \bigg[ (11)/(13)\int\limits^(10)_(-1) {(1)/(y - 11)} \, dy + (2)/(13)\int\limits^(10)_(-1) {(1)/(y + 2)} \, dy \bigg]`

Step 5: Integrate Pt. 4

Identify variables for u-substitution.

Integral 1

1. Set u:
   `\displaystyle u = y - 11`
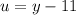
2. [u] Differentiation [Basic Power Rule, Derivative Properties]:
   `\displaystyle du = dy`
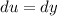
3. [Bounds] Switch:
   `\displaystyle \left \{ {{y = 10 ,\ u = 10 - 11 = -1} \atop {y = -1 ,\ u = -1 - 11 = -12}} \right.`

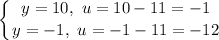
Integral 2

1. Set v:
   `\displaystyle v = y + 2`
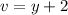
2. [v] Differentiate [Basic Power Rule, Derivative Properties]:
   `\displaystyle dv = dy`
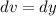
3. [Bounds] Switch:
   `\displaystyle \left \{ {{y = 10 ,\ v = 10 + 2 = 12} \atop {y = -1 ,\ v = -1 + 2 = 1}} \right.`

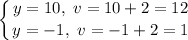
Step 6: Integrate Pt. 5

1. [Integrals] U-Substitution:
   `\displaystyle \int\limits^(10)_(-1) {(13y)/(y^2 - 9y - 22)} \, dy = 13 \bigg[ (11)/(13)\int\limits^(-1)_(-12) {(1)/(u)} \, du + (2)/(13)\int\limits^(12)_(1) {(1)/(v)} \, dv \bigg]`
2. [Integrals] Logarithmic Integration:
   `\displaystyle \int\limits^(10)_(-1) {(13y)/(y^2 - 9y - 22)} \, dy = 13 \bigg[ (11)/(13)(\ln |u|) \bigg| \limits^(-1)_(-12) + (2)/(13)(\ln |v|) \bigg| \limits^(12)_(1) \bigg]`
3. Evaluate [Integration Rule - Fundamental Theorem of Calculus 1]:
   `\displaystyle \int\limits^(10)_(-1) {(13y)/(y^2 - 9y - 22)} \, dy = 13 \bigg[ (11)/(13)[-\ln (12)] + (2)/(13)[\ln (12)] \bigg]`
4. Simplify:
   `\displaystyle \int\limits^(10)_(-1) {(13y)/(y^2 - 9y - 22)} \, dy = 11[-\ln (12)] + 2[\ln (12)]`
5. Simplify:
   `\displaystyle \int\limits^(10)_(-1) {(13y)/(y^2 - 9y - 22)} \, dy = -11\ln (12)] + 2\ln (12)`
6. Simplify:
   `\displaystyle \int\limits^(10)_(-1) {(13y)/(y^2 - 9y - 22)} \, dy = -9 \ln (12)`

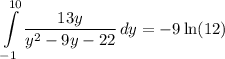
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration