Question

The scores on a Psychology exam were normally distributed with a mean of 67 and a standard deviation of 8. Create a normal distribution of these scores and answer the questions below. a. What percentage of the scores were less than 59%? b. What percentage of scores were over 83% c. If 160 students took the exam, how many students received a score over 75%?

Answer 1

(a) The percentage of the scores were less than 59% is 16%.

(b) The percentage of the scores were over 83% is 2%.

(c) The number of students who received a score over 75% is 26.

Explanation:

Let the random variable X represent the scores on a Psychology exam.

The random variable X follows a Normal distribution with mean, μ = 67 and standard deviation, σ = 8.

Assume that the maximum score is 100.

(a)

Compute the probability of the scores that were less than 59% as follows:

`P(X<59)=P((X-\mu)/(\sigma)<(59-67)/(8))`

`=P(Z<-1)\\\\=1-P(Z<1)\\\\=1-0.84134\\\\=0.15866\\\\\approx 0.16`

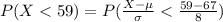
*Use a z-table.

Thus, the percentage of the scores were less than 59% is 16%.

(b)

Compute the probability of the scores that were over 83% as follows:

`P(X>83)=P((X-\mu)/(\sigma)>(83-67)/(8))`

`=P(Z>2)\\\\=1-P(Z<2)\\\\=1-0.97725\\\\=0.02275\\\\\approx 0.02`

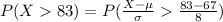
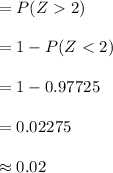
*Use a z-table.

Thus, the percentage of the scores were over 83% is 2%.

(c)

It is provided n = 160 students took the exam.

Compute the probability of the scores that were over 75% as follows:

`P(X>75)=P((X-\mu)/(\sigma)>(75-67)/(8))`

`=P(Z>1)\\\\=1-P(Z<1)\\\\=1-0.84134\\\\=0.15866\\\\\approx 0.16`

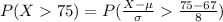
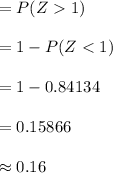
The percentage of students who received a score over 75% is 16%.

Compute the number of students who received a score over 75% as follows:

`\text{Number of Students}=0.16* 160=25.6\approx 26`

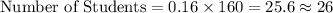
Thus, the number of students who received a score over 75% is 26.