Question

The hypotenuse of a 45°-45°-90° triangle measures 18 cm. A right triangle is shown. The other 2 angle measures are 45 degrees. The length of the hypotenuse is 18 centimeters. What is the length of one leg of the triangle? 9 cm 9 StartRoot 2 EndRoot cm 18 cm

Answer 1

Answer: D "9 StartRoot 2 EndRoot cm"

Explanation:

Edge 2021/2022, Took the test & currently taking is as this is written. Also the base is 18 and the sides usually add up to the base.

Answer 2

`9 √(2)\ cm`

Explanation:

Given

Hypotenus = 18cm

Required

Find the length of the other two sides

From the question, we understand that the other two sides are equal; let's represent them with x.

Pythagoras theorrem states that:

`Hypotenuse^2 = x^2 + x^2`

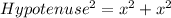
Substitute 18 for Hypotenuse

`18^2 = x^2 + x^2`

`18^2 = 2x^2`

`18 * 18 = 2x^2`

`324 = 2x^2`

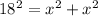
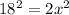
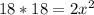
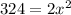
Divide both sides by 2

`(324)/(2) = (2x^2)/(2)`

`162 = x^2`

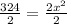
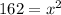
Take root of both sides

`√(162) = √(x^2)`

`√(162) = x`

`x = √(162)`

`x = √(81 * 2)`

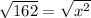
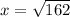
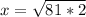
Split the above

`x = √(81) *√(2)`

`x = 9 *√(2)`

`x = 9 √(2)`

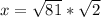
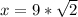
Hence, the length of one leg is
`9 √(2)\ cm`