Question

Given 4,12,20,28 find s40

Answer 1

`S_(40)=6560`

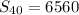
Explanation:

Given the sequence

`4,12,20,28,\cdots`

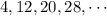
We know that:

The first term, a=4

Also, 21-4=20-12=28-20=8

Therefore, the sequence is an arithmetic sequence with:

Common difference, d=8

For an arithmetic sequence, the sum

`S_n=(n)/(2)[2a+(n-1)d] \\$Therefore$:\\\\S_(40)=(40)/(2)[2(4)+(40-1)*8] \\=20(8+39*8)\\=20(8+312)\\=20*320\\=6560`

The sum of the first 40 terms is 6560.