Question

In the figure, ABC is a quarter circle and CDEF is a square.

(a) The length of DF is 38 cm. Find the area of the square CDEF.
(b) Find the area of the shaded parts. Give your answer correct to
2 decimal places.​

Answer 1

a). 722 cm²

b). 412.11 cm²

Explanation:

ABC is a quarter circle with radius CE,

Area of a quarter circle =
`(1)/(4)\pi r^(2)`

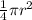
Since CDEF is a square, diagonals CE and FD will be equal.

CE ≅ FD ≅ 38cm

(a). Measure of a side of the square CDEF =
`\sqrt{(1)/(2) (\text {Diagonal})^2}`

Side =
`\sqrt{((38)^2)/(2) }`

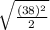
= 26.87

Area of the square CDEF = (Side)²

= (26.87)²

= 722 cm²

b). Area of the shaded part = Area of the quarter circle - Area of the square

Area of the quarter circle =
`(1)/(4)\pi (38)^(2)`

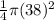
= 1134.11495 cm²

Area of the shaded area = 1134.11495 - 722

= 412.11495 cm²

≈ 412.11 cm²