Question

A rational number in its decimal expansion is 0.27575 --------. What can you say about the prime factors of q, when this number is expressed in the form p/q ? Give reasons.

Find the HCF of (6x2+ x –15) and (8x2–32x + 15)

Answer 1

The prime factors of q = 330 are 2, 3, 5 and 11.

HCF of
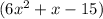`(6x^2+ x -15)` and
`(8x^2-32x + 15)` is 1.

Explanation:

First of all, let us convert the given decimal expansion in rational form.

Let Given decimal expansion:

`x =0.27575.....`

Multiply by 100:

`100x = 27.5757.......`

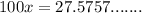
subtracting x from 100x :

`99x = 27.5757.... - 0.2757....\\\Rightarrow 99x = 27.3\\\Rightarrow 33x = 9.1\\\Rightarrow x = (9.1)/(33)\\\Rightarrow x = (91)/(330)`

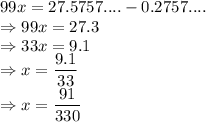
So,

`(p)/(q) = (91)/(330)`

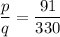
Let us make prime factors of q:

`q = 2 * 3 * 5* 11`

The prime factors of q = 330 are 2, 3, 5 and 11.

-------------

Finding HCF of
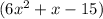`(6x^2+ x -15)` and
`(8x^2-32x + 15)`

Method to find HCF:

First of all, let us factorize them and the common part between the factors of the two will be the HCF.

`(6x^2+ x -15)\\\Rightarrow 6x^2+ 10x -9x-15\\\Rightarrow 2x(3x+ 5) -3(3x+5)\\\Rightarrow (2x -3)(3x+5)`

The factors are (2x -3) and (3x+5)

The quadratic equation
`(8x^2-32x + 15)` can not be factorized as we have factorized
`(6x^2+ x -15)`.

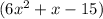`\therefore` HCF of the two is 1.