Question

You invest an initial $300 in an account that has an annual interest rate of 4%, compounded quarterly. How much money will you have in the account after 10 years? Round your answer to the nearest whole number.

Answer 1

Answer: rounded it to $447

Step-by-step explanation: i think :)

Answer 2

Explanation:

The formula you will want to use for this is one that allows a certain number of compoundings of the interest per year. This is a specific one for compounding continuously, and there is one for finding simple interest. Here is the one we want:

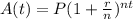`A(t)=P(1+(r)/(n))^(nt)` where A(t) is the amount in the account after the compounding occurs over the number of years specified, P is the initial amount in the account, r is the interest rate in decimal form, n is the number of times per year the compounding occurs, and t is the amount of time the money is in the account in years. For us:

P = 300,

r = .04,

n = 4 (quarterly means 4 times), and

t = 10

Filling in:

`A(t)=300(1+(.04)/(4))^((4)(10))` and

`A(t)=300(1+.01)^(40)` and

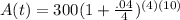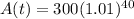`A(t)=300(1.01)^(40)` and

A(t) = 300(1.488863734) so

A(t) = $446.66 or $447