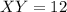Answer:
- Inverse Variation
- Equation:
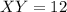
Explanation:
Given
X-> 2 | 4 | 8 | 12
Y-> 6 | 3 | 3/2 | 1
Required
- State the type of variation the table represents
- Determine the equation to model the data
To check for type of variation; we'll make use of trial by error method.
To start with; We'll check for direct variation.
This is done using the following expression;
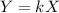 where k is the constant of variation
where k is the constant of variation
Make k the subject of formula
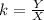
When Y = 6, X= 2
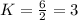
When Y = 3, X = 4
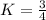
There's no need to check further as both values of k are not equal
To check for inverse variation;
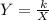
Make k the subject of formula

When Y = 6, X= 2

When Y = 3, X = 4

When Y = 3/2; X = 8
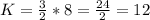
When Y = 1, X = 12

Note that for all values of X and Y, K remains constant;
Hence, the table represents an inverse direction
To determine the equation;
We make use of

Substitute 12 for k
So, the equation becomes

Reorder
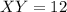
Hence, the equation is