Question

3. A box with a mass of 10.0 kg is placed on a hill that includes upwards at an angle of 30.0°.

The coefficient of static friction between the box and the hill is 0.582, which the coefficient
of kinetic friction is 0.528. If the box is given an initial push to start it moving down the hill,
will it continue moving down the hill when the initial force is removed, or will it coast to a
stop? Explain.

Answer 1

Given that,

Mass = 10 kg

Angle = 30°

Static friction = 0.582

Kinetic friction = 0.528

We need to calculate the parallel force

Using balance equation

`F =mg\sin\theta`

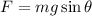
Put the value into the formula

`F= 10*9.8*\sin30`

`F = 49\ N`

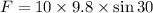
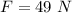
Let’s determine the two friction forces

We need to calculate the static friction force

Using static friction force

`F_(s)=\mu mg\cos\theta`

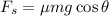
Put the value into the formula

`F_(s)=0.582*10*9.8\cos30`

`F_(s)=49.4\ N`

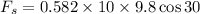
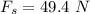
Since the box is already moving, the force of the push must be greater than difference of the force parallel and the static friction force.

We need to calculate the kinetic friction force

Using kinetic friction force

`F_(k)=\mu mg\cos\theta`

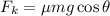
Put the value into the formula

`F_(k)=0.528*10*9.8\cos30`

`F_(k)=44.8\ N`

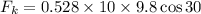
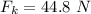
Since this friction force is less than 49 N, the box will accelerate as it moves down hill.

Hence, This is required solution.