Question

The face of the triangular concrete panel shown has an area of 22 square meters, and its base is 3 meters longer than twice its height. Find the length of the base.

Answer 1

The length of the base is 11 meters.

Explanation:

The diagram of the triangle is not shown; However, the given details are enough to solve this question.

Given

Shape: Triangle

Represent the height with h and the base with b

`b = 3 + 2h`

`Area = 22`

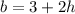
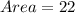
Required

Find the length of the base

The area of a triangle is calculated as thus;

`Area = (1)/(2) * b * h`

Substitute 22 for Area and 3 + 2h for b

The formula becomes

`22 = (1)/(2) * (3 + 2h) * h`

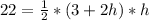
Multiply both sides by 2

`2 * 22 = 2 * (1)/(2) * (3 + 2h) * h`

`44 = (3 + 2h) * h`

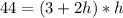
Open the bracket

`44 = 3 * h + 2h * h`

`44 = 3h + 2h^2`

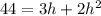
Subtract 44 from both sides

`44 - 44 = 3h + 2h^2 - 44`

`0 = 3h + 2h^2 - 44`

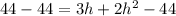
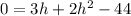
Rearrange

`0 = 2h^2 +3h - 44`

`2h^2 +3h - 44 = 0`

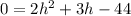
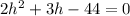
At this point, we have a quadratic equation; which is solved as follows:

`2h^2 +3h - 44 = 0`

`2h^2 + 11h - 8h - 44 = 0`

`h(2h + 11) - 4(2h + 11) = 0`

`(h - 4)(2h + 11) = 0`

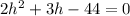
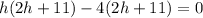
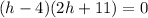
Split the above

`(h - 4) = 0\ or\ (2h + 11) = 0`

`h - 4 = 0\ or\ 2h + 11 = 0`

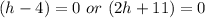
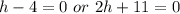
Solve the above linear equations separately

`h - 4 = 0`

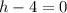
Add 4 to both sides

`h - 4 + 4 = 0 + 4`

`h = 0 + 4`

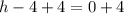
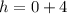
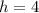`h = 4` ---- First value of h

`2h + 11 = 0`

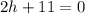
Subtract 11 from both sides

`2h + 11 - 11 = 0 - 11`

`2h = 0 - 11`

`2h = -11`

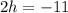
Divide both sides by 2

`(2h)/(2) = -(11)/(2)`

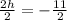
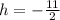`h = -(11)/(2)` ------ Second value of h

Since height can be negative, we'll discard
`h = -(11)/(2)`

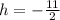
Hence, the usable value of height is
`h = 4`

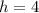
Recall that
`b = 3 + 2h`

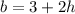
Substitute 4 for h

`b = 3 + 2(4)`

`b = 3 + 8`

`b = 11`

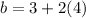
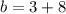
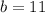
Hence, the length of the base is 11 meters