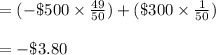Question

A raffle is set up

Ticket cost is $10. There are 50 tickets
One sole prize is $300 tablet
What is the expected value?

Answer 1

-$3.80

Explanation:

In the raffle, there are a total of 50 ticket and only one price, therefore:

The probability of winning
`=(1)/(50)`

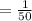
Price to be won = $300

The probability of losing
`=(49)/(50)`

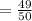
Since each ticket costs $10.

The probability distribution of the price is therefore:

`\left|\begin{array}c$Price(x)&-\$10&300\\P(x)&(49)/(50) &(1)/(50) \end{array}\right|`

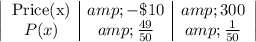
Expected Value

`=(-\$500 * (49)/(50))+(\$300*(1)/(50) )\\\\=-\$3.80`